行列のパズル

Aをm×nの実数の行列とする. Aについて好きな行または好きな列にある全ての数字の符号を一斉に変更する操作を考える. この操作を繰り返すことで, どの行の和やどの列の和がすべて負でない行列にできることを証明せよ.

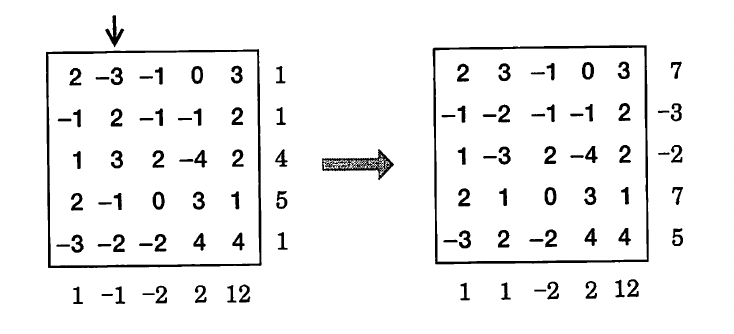
コメント

ピーター ウィンクラー著とっておきの数学パズルの8.1の問題である. この問題の元ネタは1st All Russian Mathematical Olympiad Problems 1961 Problem 7であった.

結構面白い問題なので 2023年度秋冬学期 線形代数学入門 (経(161〜)) の期末試験のおまけ問題で出した.