Kontsevichのパズル
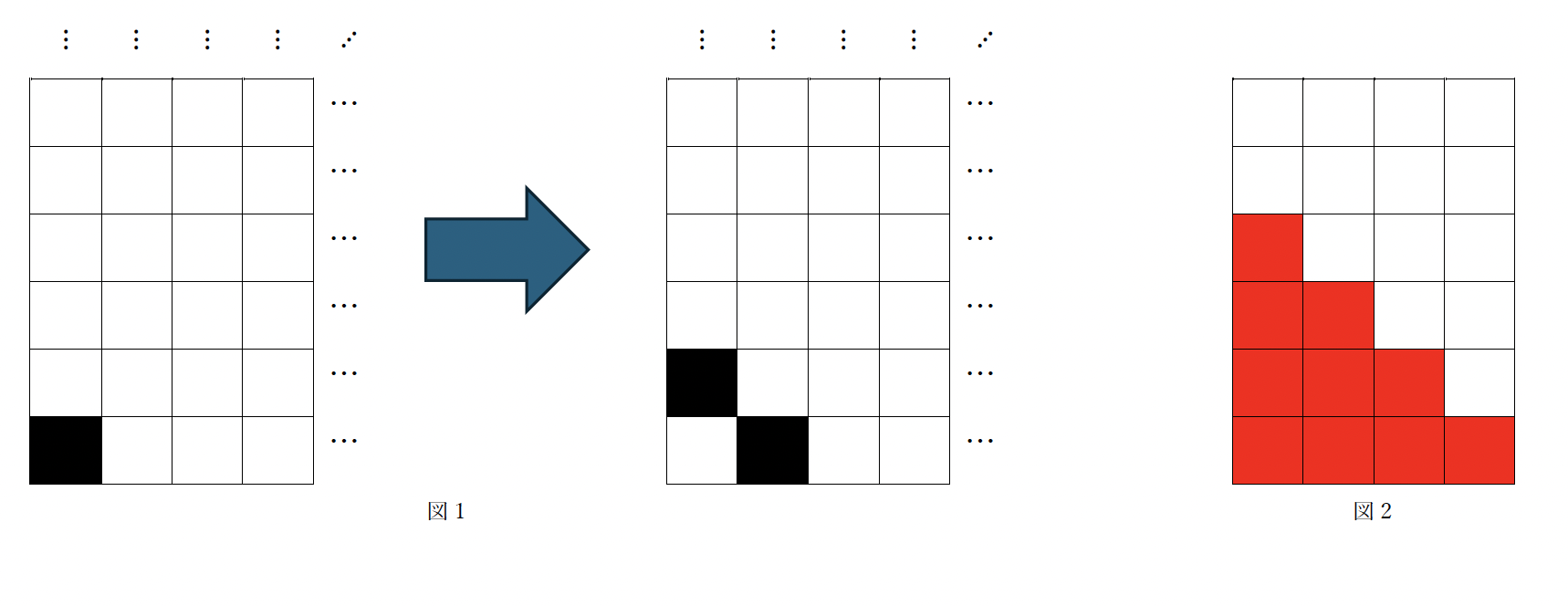
図1(下図左側)のように, 左下の1枚だけを黒タイルとし, その他のタイルは白で, それらの白タイルが上方向と右方向に無限に並んでいるものを考える. 次の操作を何回やっても, 図2(下図右側)の赤色の部分に黒のタイルがあることを示せ.
[操作] 図1のように上も右も白であるような黒のタイルを選び, それを白のタイルに変えて, その上も右も黒のタイルに変える.
コメント
元ネタはMaxim Kontsevichが1981に出したパズルEscape of the Clones. ただちょっと分かりずらいので今回はピーター・フランクルの中学生でも分かる大学生にも解けない数学の書き方に基づいた. こっちの方がわかりやすくて良い.
その後学祭にも問題を出すために上のように改良した. なおこの問題は今も研究室の前に飾っている.

コメント2
とっておきの数学パズルにも似たような問題がある(問題8.5) これはコンウェイの兵隊と呼ばれている. 私は中村先生のTAをしているときに, このコンウェイの兵隊の問題を教えてもらった.