研究内容(簡易版)
岩井雅崇(いわいまさたか)と申します. 大阪大学理学研究科数学専攻の准教授です. Link
専門は複素幾何学, 代数幾何学, 多変数複素解析です. 主に以下のことに興味があります.
- 接ベクトル束が正値性を持つ代数多様体の構造. 接ベクトル束や葉層が「豊富・ネフ・巨大・擬有効」である場合の代数多様体の構造を明らかにした. log版や特異多様体(KLT多様体)にも拡張した.
- 余接ベクトル束が正値性を持つ代数多様体の構造. 数値的小平次元が1以下の余接ベクトル束がネフな代数多様体に関して, アバンダンス予想が正しいことを示し, その場合の代数多様体の構造を明らかにした.
- 第2チャーン類と構造定理. Miyaoka-Yau不等式のような第2チャーン類に関する不等式をいくつか示し, さらにその等号が成立するときの代数多様体の構造を明らかにした.
大阪大学のスタッフのページにも詳しく書きました.
研究内容(詳しい版)
研究内容・教科書一覧・お役立ち情報をまとめました.
分割版
上はかなり長いんで, 三つに分けました
2の教科書一覧は私の周りの分野の教科書をまとめました. これはめちゃくちゃ頑張りました. 複素幾何など複素数体上の代数・幾何・解析を目指す人はぜひ見てほしいです. また専門家の人はいい教科書があれば教えてください. 増やしていきます.
1の研究内容はこの図を頑張って書きました. chat GPTに原型を作ってもらって, その後ちょっと加工しました. ほとんどのデータはMathematics Genealogy Projectによります.
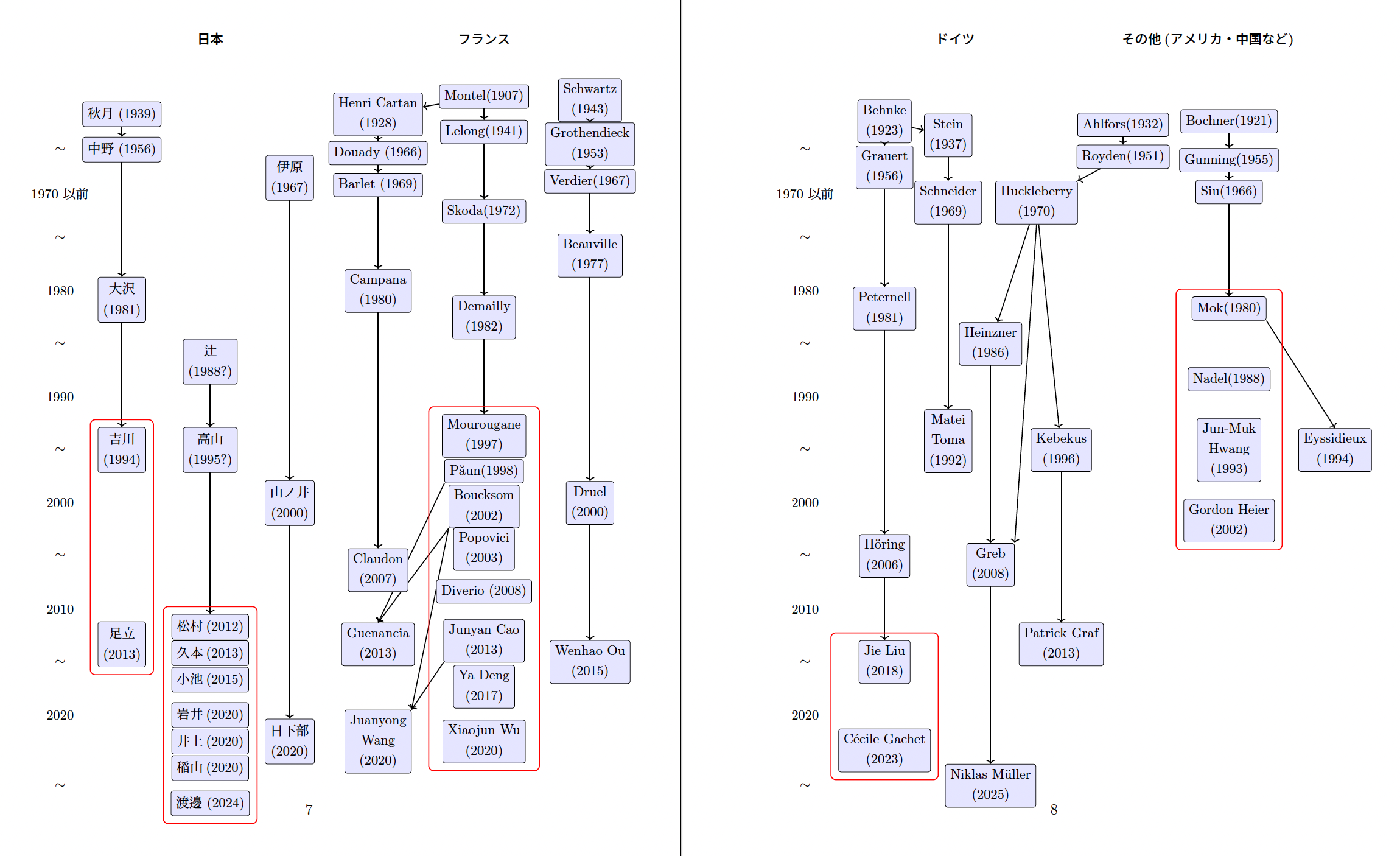
高山先生・辻先生の指導教官に関しては辻先生・大沢先生から聞いた情報になります. そのためもしかすると博士取得時の(形式的な)指導教官は別である可能性もあります. また岩井含め高山研出身の人はMathematics Genealogy Projectに載っていない研究者になります.
3は説教くさいの読んでも読まなくてもいいです. 不要な部分は無視して必要な部分だけ取り入れてください.