Kontsevich’s puzzle

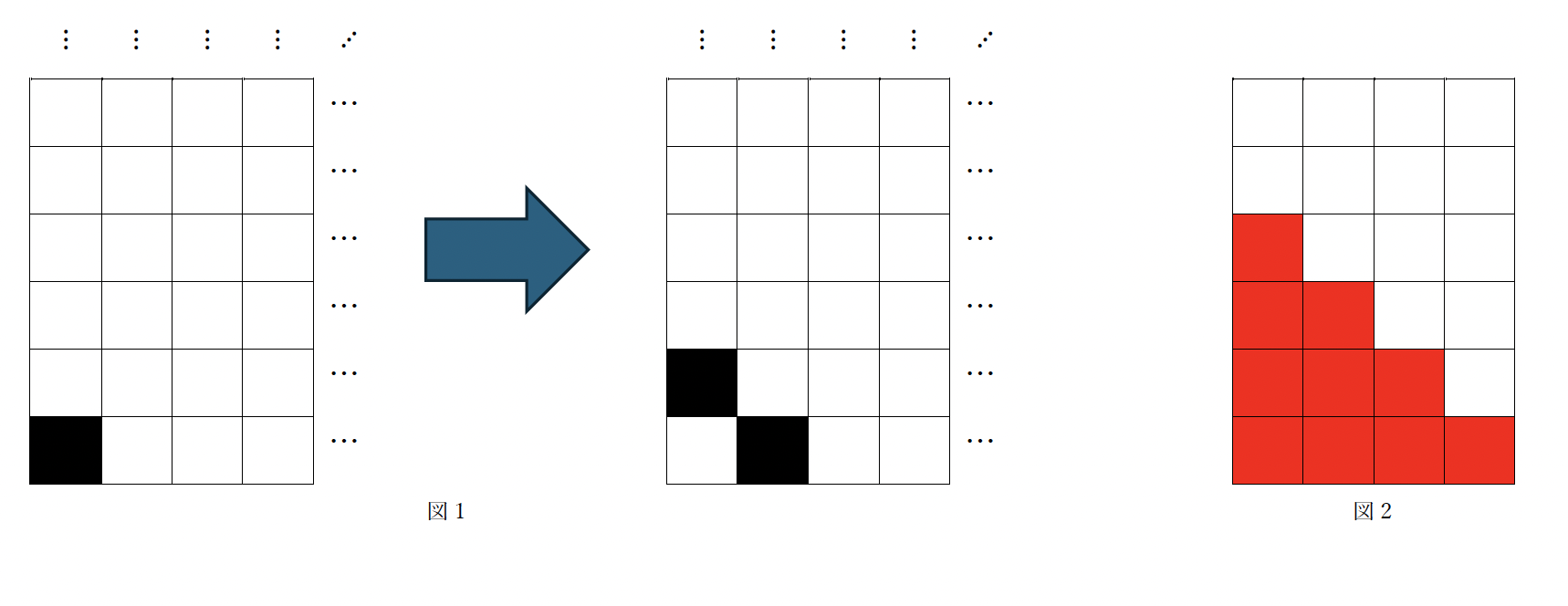
As in Figure 1 (on the left below), consider a grid where only the bottom-left tile is black, and all other tiles are white, with these white tiles extending infinitely upward and to the right. Show that, no matter how many times you apply the following operation, there will always be a black tile in the red region shown in Figure 2 (on the right below).

[Operation] Choose a black tile whose tile above and tile to the right are both white (as in Figure 1). Change this chosen tile to white, and change both the tile above and the tile to the right to black.

Comments

This puzzle is based on the Maxim Kontsevich’s puzzle in 1981: Escape of the Clones. I used this puzzle for our school festival. Even now, this problem is displayed in front of my laboratory.